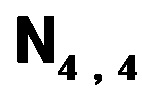UNIDAD II - ENCRIPTACIÓN CON MATRICES

UNIDAD II - INVERSA DE UNA MATRIZ

UNIDAD II - DETERMINANTE DE MATRICES

UNIDAD II - DIAGONALIZAR UNA MATRIZ

UNIDAD II - MULTIPLICACIÓN DE MATRICES

La multiplicación de matrices es un procedimiento enredoso y hasta un poco complicado de entender si no se tiene aun la practica necesaria, por lo que hay pequeños "trucos" que nos ayudaran a determinar rápidamente si se puede o no realizar una multiplicación.

1.- Lo primero es observar el tamaño de nuestra primer matriz. Y el tamaño de nuestra segunda matriz.
Una vez tengamos sus tamaños definidos, tenemos que comprobar que el numero de columnas de la primera, sea igual al numero de renglones de la segunda.

Supongamos una matriz principal de 3 x 3. La cual queremos multiplicar por una matriz de 2 x 3. Observamos lo siguiente:

Como podemos apreciar dichas matrices  no son multiplicables entre si. Por lo que únicamente se deja indicado.

Ahora supongamos unas matrices que si se pueden multiplicar, una principal de tamaño 3 x 2 y una matriz secundaria de 2 x 3.

Como se puede apreciar si se pueden multiplicar, entonces pasamos con nuestro siguiente paso.

2.- Una vez verifiquemos que si es posible multiplicar las matrices, tenemos que saber cual va a ser el tamaño de la matriz resultante una vez terminemos con nuestras operaciones.

Esto lo hacemos de la siguiente manera. Tomamos el numero de filas de la primer matriz, y lo unimos con el numero de columnas de la segunda.

La matriz resultante seria entonces de 3 x 3.

Ahora si procedemos a realizar las operaciones. Multiplicando la fila de la primera por la columna de la segunda. Pero en que orden?

Observemos que nuestra matriz resultado tiene marcadas sus posiciones, esto es muy útil ya que utilizaremos los valores de estas posiciones para saber con exactitud que fila y que columna multiplicar.

Entonces tomemos la primer posición C 1,1. Ahora el primer numero indica la primer fila de la primer matriz, y el siguiente indica la primer columna de la segunda matriz.

Si aun no te queda claro, tomemos otro valor, por ejemplo C 2,3. El resultado en esa posición sera la multiplicación de la 2 fila de la primer matriz, por la 3 columna de la segunda matriz.

En el caso de la C 3,3 sera: la 3 fila de la primer matriz por la 3 columna de la segunda matriz.

Se tiene que entender que todo esto, se va adquiriendo poco a poco con la practica continua de ejercicios, por lo que si no se entiende a la primera, no hay que desistir y continuar practicando.

Como podemos ver, y no solo en esta si no en todas las multiplicaciones de matrices. Los datos de la primer columna encajan exactamente con los datos de la segunda.

Es decir, para cada valor de la fila, tenemos la misma cantidad de valores para la columna:

Cada "enlace" de números serán multiplicados, formando grupos.

Y los resultados de cada grupo se suman, generando el valor de la posición indicada.

Hagamos el resultado de lo siguiente:

Obtener el valor de la posición C 3,2.
3 Fila de la primer matriz.
2 Columna de la segunda matriz.

Ahora formamos los grupos de cada una de ellas.

Primer "enlace" (7)(2) = 14.

Segundo "enlace" (8)(5) = 40.

Sumando los resultados de cada grupo = 54.

Ese sera el resultado de la posición C 3,2.

Para calcular las siguientes posiciones se realizara el mismo procedimiento.

Te dejamos el resultado de la matriz C, para que tu realices las multiplicaciones y las compruebes con estos resultados:

UNIDAD II - SUMA Y RESTA DE MATRICES

La suma y resta de matrices se realiza siempre y cuando el tamaño de las matrices sea el mismo.

No necesariamente estas tienen que ser cuadradas.

Supongamos una matriz A (3 x 3) y una matriz B (3 x 3). Como se puede apreciar el tamaño de estas es igual, por lo tanto se podrá sumar o restar.

Si alguna de las matrices hubiese sido de tamaño (4 x 2), estas no se habrían podido sumar, ya que no cumplirían la regla. Ser exactamente iguales en su tamaño.

Para realizar la siguiente operación, únicamente se tiene que sumar el numero, en la posición de la matriz A, por el numero, en la misma posición de la matriz B.

Es decir, si quiero sumar la posición A 1,1 , este tiene un valor de 2. Tendría que sumarle el valor de la posición B 1,1 que es de 1. Por lo tanto en la matriz resultante el valor sera de 3.

Esto se tiene que realizar con cada una de las posiciones. Una por una y de manera directa.

Lo mismo sucede con la resta, únicamente se cambia el símbolo operador por una resta.

Siguiendo el ejemplo si quiero restar la posición de A 1,3 con valor 1. Tendría que restarle el valor de B 1,3 con valor de 1. Por lo tanto el resultado sera de 0.

UNIDAD II - TIPOS DE MATRICES

Al ser la matriz un conjunto de números, ordenados por filas y columnas, es normal que se hagan distintas combinaciones de tamaños.

En las siguientes imágenes podrás observar distintos tipos de matrices que pueden formarse y como identificarlas.

MATRIZ COLUMNA

Su nombre se debe, a obvias razones. Únicamente cuenta con 1 columna.

Puede ir desde 1 fila hasta n (filas). es decir no se limita a cierto numero de filas, siempre y cuando mantenga esta condición: Contar solo con 1 columna.

MATRIZ RENGLÓN

Al igual que la matriz columna, esta tiene una característica, y es que debe contar únicamente con 1 fila.

Caso contrario con la matriz anterior, esta puede tener n(columnas) pero únicamente la fila principal, eh de ahí su nombre renglón.

MATRIZ CUADRADA

Con estos 3 ejemplos podemos observar una característica que comparten las 3.

Para que la matriz, sea del orden cuadrada; el numero de columnas de esta debe ser exactamente igual a su numero de filas.

Las matrices cuadradas serán entonces: 2 filas por 2 columnas (2 x 2), 3 x 3, ... n = m.

MATRIZ NULA

Se dice que una matriz es nula, cuando todos los elementos dentro de esta son ceros.

MATRIZ TRANSPUESTA

Se le denomina de esta manera, a la matriz que resulte de:

Intercambiar, el contenido de una fila, a modo columna. Ejemplo:

1.- Si  a nuestra matriz principal  (A)  de tamaño 3 x 2, le intercambiamos renglones por columnas la matriz resultante será matriz transpuesta de A ( AT ).

2.- Al transponer una matriz podemos cambiar el tamaño de la misma. Tomando A (3 x 2) al transponer los valores, queda AT con un tamaño de (2 x 3).

MATRIZ TRIANGULAR SUPERIOR

Esta matriz contiene valores nulos (0), por debajo de su diagonal principal, y únicamente es valido para matrices cuadradas.

MATRIZ TRIANGULAR INFERIOR

De igual manera esta cuanta con valores nulos (0), pero caso contrario a la triangular superior, esta los contendrá por encima de su diagonal principal.

UNIDAD II - MATRICES

INTRODUCCIÓN

Se le denomina matriz al conjunto numérico, ordenado por filas y columnas.

La notación correcta para saber el tamaño de una matriz, se determina colocando un subíndice,que sera el valor total de filas que la compone (i); una coma, y seguido el número total de columnas de la misma matriz(j).

Utilizando la matriz de ejemplo anterior, su notación quedaría de la siguiente manera:

La notación anterior nos hace referencia a una matriz de tamaño 4 filas por 4 columnas.